Trained agent plays Tetris with above average competence, winning more often than it loses.

In what proved to be my most challenging reinforcement learning project to date, I set about letting an agent teach itself to play tetris. As ever, reinforcement learning proves to be as much dark magic as science, requiring an almost telepathic empathy with the agent to nudge it in the right direction.

This is a guide to some of the key components to building out a successful reinforcement learning solution. You can find all the code to replicate my results in a public repo, and you’re welcome to use this project as a template for other experiments in reinforcement learning.

1) Tetris#

Step 1 is getting Tetris up and running. There seem to be many third-party options to save ourselves the effort of cloning Tetris from scratch, but that’s not really how we do things around here. In any case, in RL it pays to have your hands on the nuts and bolts, and that usually means making your own simulation.

Inspired by the kinds of hyper-efficient bitfield operations used in state-of-the-art chess engines (watch out for an upcoming project), I chose to implement both individual tetriminoes and the field of those already fallen using a common Field class.

The dunder methods used below permit some very pleasing operations:

if falling_shape & fallen_shapes tests whether two fields collide.
if shape & (left_edge | right_edge | bottom_edge) tests whether a shape is touching any of the edges
new_field = falling_shape + fallen_shapes gives a new field with the bits of both fields set.

class Field:
    @staticmethod
    def left_edge():
        field = Field(height=HEIGHT, width=WIDTH)
        for row in field.field:
            row[0] = 1
        return field
    
    @staticmethod
    def right_edge():
        field = Field(height=HEIGHT, width=WIDTH)
        for row in field.field:
            row[-1] = 1
        return field
    
    @staticmethod
    def bottom_edge():
        field = Field(height=HEIGHT, width=WIDTH)
        field.field[-1] = 1
        return field

    def __init__(self, height=HEIGHT, width=WIDTH, field=None):
        self.height = height
        self.width = width
        if field is not None:
            self.field = field
        else:
            self.field = np.zeros((height, width), dtype=float)

    def __bool__(self):
        return bool(self.field.astype(bool).any())

    def __and__(self, other):
        if not isinstance(other, Field):
            return NotImplemented
        field = Field(
            field=self.field.astype(bool) & other.field.astype(bool)
        )
        return field
    
    def __or__(self, other):
        if not isinstance(other, Field):
            return NotImplemented
        field = Field(
            field=self.field.astype(bool) | other.field.astype(bool)
        )
        return field
    
    def __add__(self, other):
        if not isinstance(other, Field):
            return NotImplemented
        field = Field(
            field=self.field + other.field
        )
        return field
    
    def translate(self, y=0, x=0):
        self.field = np.roll(self.field, (y, x), axis=(0, 1))
        return self
        
    def clear(self):
        self.field.fill(0)
        return self
    
    def display(self):
        plt.imshow(self.field)

For the rest of the code, feel free to browse the repository.

2) Environment#

The environment is the agent’s interface with the game. The environment takes actions, and returns rewards, metadata, and a representation of the game’s state.

Actions#

In each timestep, the agent has a choice of 5 actions:

0: do nothing
1: try to move the tetrimino to the left
2: try to move the tetrimino to the right
3: try to rotate the tetrimino clockwise
4: try to rotate the tetrimino anticlockwise

State#

This is what the agent “sees”. I ultimately arrived at a three-channel representation of the board in binary (just 1s and 0s), with some extra engineered features. We can plot it like this:

State: what the agent sees. There are three sections: the tetris grid (top plots), engineered features (bottom plots), and the upcoming tetrimino queue (not pictured). The grid and engineered features comprise three channels: current fallen shapes; current falling shape; and the current falling shape projected down onto the current fallen shapes.

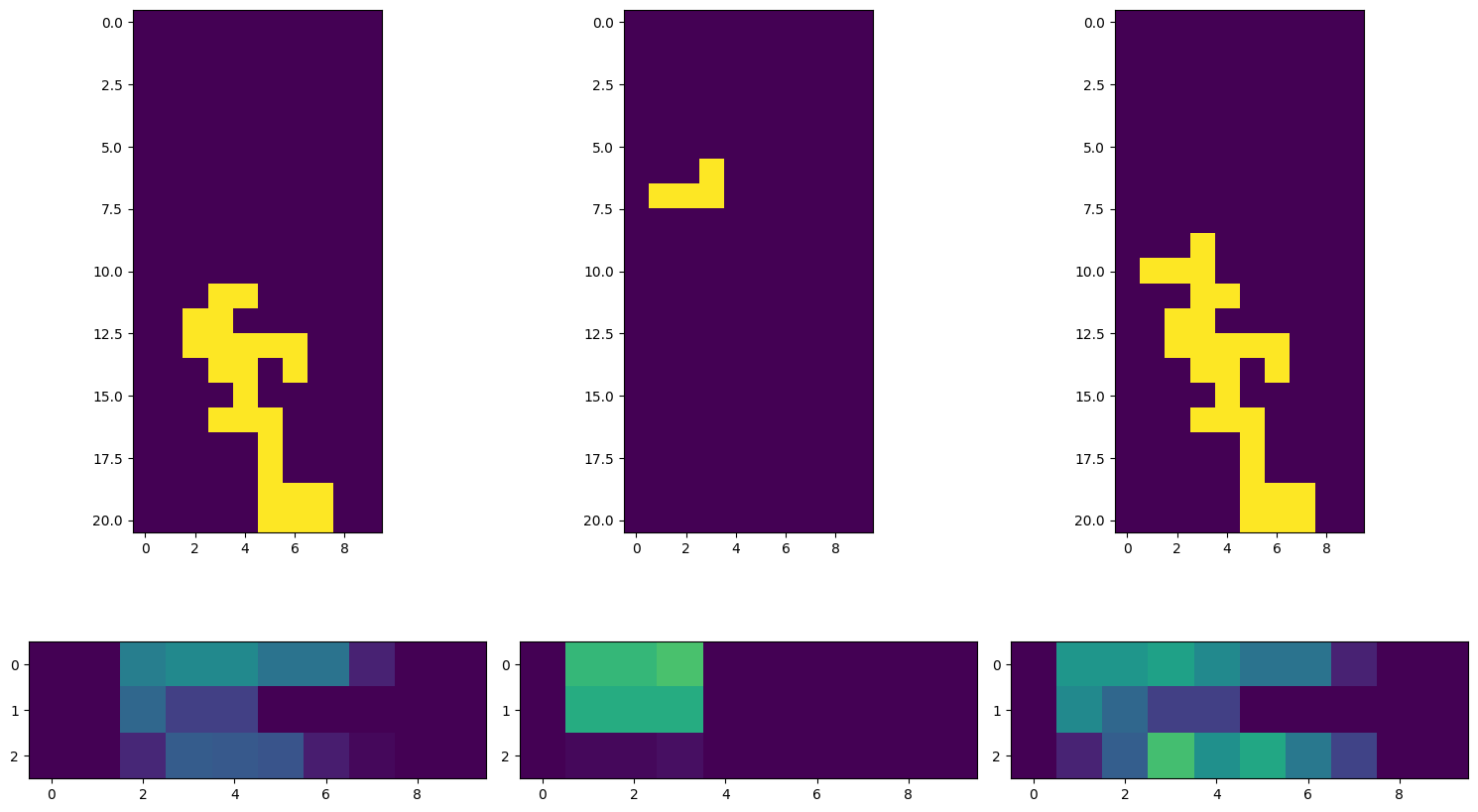
Engineered features include:

The minimum and maximum heights of the fallen field in each column
The densities of each of the columns of the fallen field

These are intended to give the agent some high-level information about the field. Whilst I experimented with providing the agent with the grid as a 3-channel 2d array, for consumption via a CNN, this proved no more effective than a flattened vector into an MLP, but much slower.

Rewards#

Whilst in my experiments agents certainly showed evidence of training when given only primary rewards (ie points for clearing lines and penalties for losing games), training proceeds much more quickly when shaping rewards are used to nudge the agent towards successful behaviour.

This is especially relevant in a game like tetris because:

a) rewards are very sparse: there are likely hundreds of game steps between line clearances
b) random play is exceedingly unlikely to result in line clearances

The downside of shaping rewards is that they can motivate unintended behaviour. I found that certain shaping rewards resulted in agents that, for example, prioritised efficient packing of tetriminoes rather than line clearances.

In the end, I found that the following reward structure resulted in successful training. In addition to the primary line clearance rewards, we penalise the agent for increasing the field’s height, and also for creating overhangs. Small rewards are available for not doing these things, as well as for partially filling lines.

line_clear_rewards = np.array([0, 1, 3, 5, 8])
height_penalty = -1
no_height_reward = 0.5
overhang_penalty = -0.5
no_overhang_reward = 0.25
loss_penalty = -1
line_shaping_rewards = {
    0: 0,
    1: 0,
    2: 0,
    3: 0,
    4: 0,
    5: 0.02,
    6: 0.04,
    7: 0.06,
    8: 0.08,
    9: 0.10,
}

You might be surprised to see that the loss signal is so small (just -1). I found that a large loss penalty was counterproductive in this reward structure, since losing behaviour (ie increasing the field’s height) is already heavily penalised, and much more immediately than a single terminal state penalty.

These shaping rewards mean that we need to calculate lots of metadata about the tetris field. Fortunately this can all be done very neatly using numpy operations.

def get_heights(self, field):
    max_height = 21
    a = field.T
    a = np.where((a > 0) & (a < 1), 1, 0)
    heights = np.zeros(10)
    for i in range(10):
        h = np.argmax(a[i])
        if h != 0:
            heights[i] = max_height - h
    return heights

def get_max_height(self):
    return int(self.get_heights(self.game.field.field).max())

def get_min_max_heights(self, field):
    f = field.field
    max_height = f.shape[0]
    a = f.T.astype(bool).astype(int)
    any_placed = a.any(axis=1)

    max_heights = np.where(
        any_placed,
        max_height - np.argmax(a, axis=1),
        0,
    ) / max_height

    b = np.flip(a, axis=1)

    any_placed = b.any(axis=1)

    min_heights = np.where(
        any_placed,
        np.argmax(b, axis=1),
        0,
    ) / max_height

    return np.concatenate([max_heights, min_heights])
        
def get_line_sums(self):
    return self.game.field.field.astype(bool).astype(int).sum(axis=1)

def get_overhangs(self):
    diff = np.diff(self.game.field.field.astype(bool).astype(int), axis=0)
    return np.sum(diff == -1, axis=0).sum()

In our environment class’ step function, we need to carefully calculate rewards associated with each action. In our case, rewards only apply when shapes are placed (or when the game is lost), so we need to detect that. Then we need to detect a change in the maximum height, the number of overhangs, and the density of each line.

def step(self, action):
    shape_landed, lines_cleared, terminated = self.game.step(action)
    self.lines_cleared += lines_cleared

    reward = 0
    truncated = False

    if self.lines_cleared >= self.win_lines_cleared:
        reward = self.line_clear_rewards[lines_cleared]
        terminated = True

    elif terminated:
        reward = self.loss_penalty

    else:
        if shape_landed:
            if lines_cleared == 0:
                max_height = self.get_max_height()
                if max_height > self.last_max_height:
                    height_change = max_height - self.last_max_height
                    reward += height_change * self.height_penalty
                    self.last_max_height = max_height
                else:
                    reward += self.no_height_reward

                line_sums = self.get_line_sums()
                new_line_sums = line_sums[line_sums != self.last_line_sums]
                for line_sum in new_line_sums:
                    reward += self.line_shaping_rewards[line_sum]
                self.last_line_sums = line_sums

                overhangs = self.get_overhangs()
                if overhangs != self.last_overhangs:
                    new_overhangs = overhangs - self.last_overhangs
                    reward += new_overhangs * self.overhang_penalty
                    self.last_overhangs = overhangs
                else:
                    reward += self.no_overhang_reward

            else:
                reward = self.line_clear_rewards[lines_cleared]
                self.last_max_height = self.get_max_height()
                self.last_line_sums = self.get_line_sums()
                self.last_overhangs = self.get_overhangs()
            
    state = self.get_state()

    info = {}
    
    return state, reward, terminated, truncated, info

3) Training#

I used the stable-baselines3 library to train a number of different models. I tried PPOs, CNNs, autoencoders, and some fairly exotic model architectures – but in the end I had most success with a fairly straightforward DQN setup fed a flattened version of the state. You can find the entirety of my training script below:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import time
import os

from stable_baselines3.common.vec_env import VecNormalize, DummyVecEnv, VecTransposeImage
from stable_baselines3.common.monitor import Monitor
from stable_baselines3 import DQN
from stable_baselines3.common.evaluation import evaluate_policy
from stable_baselines3.common.callbacks import EvalCallback, BaseCallback
from stable_baselines3.common.monitor import Monitor
from stable_baselines3.common.vec_env import SubprocVecEnv
from stable_baselines3.common.torch_layers import BaseFeaturesExtractor

import torch as th
import torch.nn as nn

import src.env
from src.utils import linear_schedule, exponential_schedule


HEIGHT, WIDTH = 21, 10
STATE_MODE = 1
CHANNELS = 3


def make_env(rank, seed=0):
    def _init():
        env = src.env.TetrisEnv(state_mode=STATE_MODE, channels=CHANNELS)
        return Monitor(env)
    return _init


N_ENVS = 8
N_TIME_STEPS = 25_000_000
NORM_OBS = False
NORM_REWARD = False

net_arch = [256, 256, 256, 256, 256,]
policy_kwargs = dict(
    net_arch=net_arch
)
model_kwargs = dict(
    learning_rate=exponential_schedule(1e-5),
    exploration_fraction=1.0,
    exploration_initial_eps=0.05,
    exploration_final_eps=0.01,
    buffer_size=500_000,
    learning_starts=250_000,
    gamma=0.999,
    train_freq=4,
    tau=1.0,
    batch_size=128,
    device="cpu",
    verbose=1,
)

env_fns = [make_env(i) for i in range(N_ENVS)]
vec_env = SubprocVecEnv(env_fns)
vec_normalise_env = VecNormalize(vec_env, norm_obs=NORM_OBS, norm_reward=NORM_REWARD)

eval_env = DummyVecEnv([lambda: make_env(0)()])
eval_env = VecNormalize(eval_env, norm_obs=NORM_OBS, norm_reward=NORM_REWARD, training=False)

load_path = "./models/DQN/v7/final_model"
model_path = "./models/DQN/v8"
os.makedirs(model_path, exist_ok=True)

if load_path is not None:
    model = DQN.load(
        path=load_path,
        env=vec_normalise_env, 
        **model_kwargs
    )
else:
    model = DQN(
        'MultiInputPolicy',
        env=vec_normalise_env, 
        policy_kwargs=policy_kwargs,
        **model_kwargs
    )

# Evaluate and continue training
eval_callback = EvalCallback(
    eval_env, best_model_save_path=model_path,
    log_path=model_path, eval_freq=10_000,
    n_eval_episodes=20, deterministic=True, render=False,
)

# Continue training the loaded or new model
model.learn(total_timesteps=N_TIME_STEPS, callback=eval_callback, reset_num_timesteps=True)
model.save(os.path.join(model_path, 'final_model.zip'))

4) Results#

In addition to watching the agent play Tetris, as seen at the top of this page, it is also useful to run a benchmarking / diagnostics script to understand the agent’s progress.

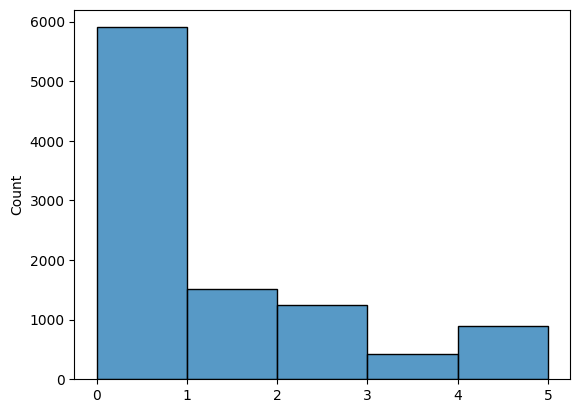
In a 10,000 timestep game, we can see that the trained agent chooses to take no action about 60% of the time. This is a good thing, as it means the agent is confidently letting the shape fall into position. It chooses left and right roughly an equal amount, but interestingly has a bias to rotate in one direction more than the other. It might be that the agent has simply learnt to always rotate shapes with two degrees of symmetry in one direction.

Distribution of actions chosen by trained agent

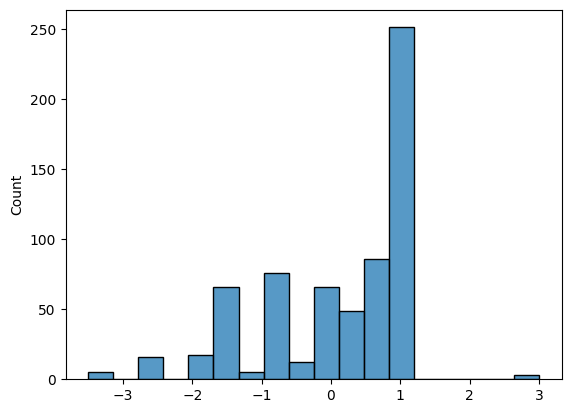
It is also very useful to inspect the distribution of rewards. I’ve often found forms of normalisation usually recommended in machine learning to be detrimental in reinforcement learning, so with normalisation disabled it’s important to ‘manually’ normalise the rewards towards something vaguely resembling a normal distribution – though the distribution will completely change as the agent learns more optimal behaviour.

Distribution of rewards gained by trained agent

In the end, it took many tens of millions of timesteps of training for the agent to start winning more often that it lost. With more training, and additional model complexity, more performance could no doubt be unlocked. But it turns out that even the humble game of Tetris is sufficiently challenging for a reinforcement learning algorithm to master; and that true mastery of Tetris would probably require significant investment in cloud GPU resource.

Training an AI to play Tetris using Deep Reinforcement Learning